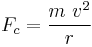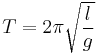Christiaan Huygens
| Christiaan Huygens | |
|---|---|
Christiaan Huygens
|
|
| Born | 14 April 1629 The Hague, Netherlands |
| Died | 8 March 1695 (aged 65) Netherlands |
| Residence | Netherlands, France |
| Nationality | Dutch |
| Fields | Physics Mathematics Astronomy Horology Science fiction |
| Institutions | Royal Society of London French Academy of Sciences |
| Alma mater | University of Leiden College of Orange |
| Doctoral advisor | Frans van Schooten John Pell |
| Known for | Titan Explanation Saturn's rings Centrifugal force Collision formulae Pendulum clock Huygens–Fresnel principle Wave theory Birefringence First theoretical physicist |
| Influences | René Descartes Frans van Schooten Blaise Pascal Marin Mersenne |
| Influenced | Gottfried Wilhelm Leibniz Isaac Newton |
Christiaan Huygens, FRS (English pronunciation: /ˈhaɪɡənz/, [ˈɦœyɣə(n)s] ( listen); (14 April 1629 – 8 July 1695) was a prominent Dutch mathematician, astronomer, physicist and horologist. His work included early telescopic studies elucidating the nature of the rings of Saturn and the discovery of its moon Titan, the invention of the pendulum clock and other investigations in timekeeping, and studies of both optics and the centrifugal force.
Huygens achieved note for his argument that light consists of waves,[1] now known as the Huygens–Fresnel principle, which two centuries later became instrumental in the understanding of wave-particle duality. He generally receives credit for his discovery of the centrifugal force, the laws for collision of bodies, for his role in the development of modern calculus and his original observations on sound perception (see repetition pitch). Huygens is seen as the first theoretical physicist as he was the first to use formulae in physics.
Contents |
Life
Christiaan Huygens was born in April 1629 at The Hague, the second son of Constantijn Huygens, (1596–1687), a friend of mathematician and philosopher René Descartes, and of Suzanna van Baerle (deceased 1637), whom Constantijn had married on 6 April 1627. Christiaan studied law and mathematics at the University of Leiden and the College of Orange in Breda. After a stint as a diplomat, Huygens turned to science.
French Academy of Sciences and Royal Society
The Royal Society elected Huygens a member in 1663. In the year 1666, Huygens moved to Paris where he held a position at the French Academy of Sciences under the patronage of Louis XIV. Using the Paris Observatory (completed in 1672), he made further astronomical observations. In 1678 he introduced Nicolaas Hartsoeker to French scientists such as Nicolas Malebranche and Giovanni Cassini. In 1684, he published "Astroscopia Compendiaria" which presented his new aerial (tubeless) telescope.
Death
Huygens moved back to The Hague in 1681 after suffering serious illness. He attempted to return to France in 1685 but the revocation of the Edict of Nantes precluded this move. Huygens died in The Hague on 8 July 1695, and was buried in Grote Kerk.[2]
Scientific work
Mathematics
Probability theory
After Blaise Pascal encouraged him to do so, Huygens wrote the first book on probability theory,[3] De ratiociniis in ludo aleae ("On Reasoning in Games of Chance"),[4] which he had published in 1657.
Physics
Mechanics
Huygens formulated what is now known as the second law of motion of Isaac Newton in a quadratic form . Newton reformulated and generalized that law. In 1659 Huygens derived the now well-known formula for the centripetal force, exerted by an object describing a circular motion, for instance on the string to which it is attached, in modern notation:
with m the mass of the object, v the velocity and r the radius. Furthermore, Huygens concluded that Descartes' laws for the elastic collision of two bodies must be wrong and formulated the correct laws .
Wave theory
Huygens is remembered especially for his wave theory of light, which he first communicated in 1678 to France's Royal Academy of Sciences and which he published in 1690 in his Treatise on light (see also Huygens-Fresnel principle).[5] The later theory of light by Isaac Newton in his Opticks proposed a different explanation for reflection, refraction and interference of light assuming the existence of light particles. The interference experiments of Thomas Young vindicated Huygens' wave theory in 1801, as the results could no longer be explained with light particles (see however wave-particle duality).
Optics
Huygens experimented with double refraction (birefringence) in Icelandic crystal (calcite) and explained it with his wavetheory and polarised light. He also investigated the use of lenses as projectors and should be credited as the earliest inventor, developer and designer of the Magic Lantern rather than German scholar Athanasius Kircher who merely used much of Huygens research (often quite inaccurately) to document and publish on the subject.
Clocks
He also designed more accurate clocks than were available at the time, suitable for sea navigation. His invention of the pendulum clock, patented in 1657, was a breakthrough in timekeeping. Huygens is not known ever to have made a clock himself, however; he contracted the construction of his designs to Salomon Coster in The Hague.
In 1673 he published his mathematical analysis of pendulums, Horologium Oscillatorium sive de motu pendulorum, his greatest work on horology. It had been observed by Marin Mersenne and others[8][9] that pendulums are not quite isochronous, that is, their period depends on their width of swing, wide swings taking longer than narrow swings. Huygens analysed this problem by finding the shape of the curve down which a mass will slide under the influence of gravity in the same amount of time, regardless of its starting point; the so-called tautochrone problem. By geometrical methods which were an early use of calculus, he showed that this curve is a cycloid, not the circular arc of a pendulum's bob, so pendulums are not isochronous. He also solved the problem posed by Mersenne of how to calculate the period of a pendulum made of an arbitrarily shaped swinging rigid body, discovering the center of oscillation and its reciprocal relationship with the pivot point. In the same work, he analysed the conical pendulum, consisting of a weight on a cord moving in a circle, using the concept of centrifugal force.
Huygens was the first to derive the formula for the period of an ideal mathematical pendulum (with massless rod or cord), in modern notation:
with T the period, l the length of the pendulum and g the gravitational acceleration.
Huygens also observed that two of his pendulum clocks mounted next to each other on the same support often become synchronized, swinging in opposite directions. He reported the results by letter to the Royal Society of London and it is referred to it as "an odd kind of sympathy" in the Society's minutes.[10][11] This may be the first published observation of what is now called coupled oscillations.
The oldest known Huygens style pendulum clock is dated 1657 and can be seen at the Museum Boerhaave in Leiden[12][13][14][15] which also shows an important astronomical clock owned and used by Huygens.
Huygens developed a balance spring watch more or less contemporaneously with, though separately from, Robert Hooke, and controversy over who should be given credit for this important invention persisted for centuries. This is because Huygens watches employed a spiral balance spring. However, it should be noted that Huygens used this form of spring initially only because the balance in his first watch rotated more than one and a half turns. He later used spiral springs in more conventional watches, made for him by Thuret in Paris from around 1675.
Such springs are essential in modern watches with a detached lever escapement because they can be adjusted for isochronism. Based on this fact, many writers in the past and even the present have given Huygens the credit for inventing the modern form of spiral balance spring in 1675 rather than Hooke's earlier straight spring of 1665 because they considered that the spiral form automatically conferred the property of isochronism on the oscillating balance. However, this assumption is incorrect, as all watches in the time of Huygens and Hooke employed the very un-detached verge escapement, the action of which destroys the isochronal properties of any form of balance spring, spiral or otherwise.
In February 2006, a long-lost copy of Hooke's handwritten notes from several decades of Royal Society meetings was discovered in a cupboard in Hampshire, and the balance-spring controversy appears, by evidence contained in those notes, to be settled in favour of Hooke's claim.[16][17]
The watches which were made in Paris from C.1675 and following Huygens plan, are notable for lacking a fusee for equalizing the mainspring torque, showing that Huygens thought that his spiral spring would isochronise the balance, in the same way that he thought that the cycloidally shaped suspension curbs on his clocks would isochronise the pendulum.
Internal combustion and other inventions
In 1673, Huygens carried out experiments with internal combustion. Although he designed a basic form of internal combustion engine, fueled by gunpowder, he never successfully built one.Even though he was unsuccessful with building his internal combustion engine he had given many other scientist the capability to do so.
In 1675, Christiaan Huygens patented a pocket watch. He also invented numerous other devices, including a 31-tone-to-the-octave keyboard instrument that made use of his discovery of 31 equal temperament.
Astronomy
Saturn's rings and Titan
In 1655, Huygens proposed that Saturn was surrounded by a solid ring, "a thin, flat ring, nowhere touching, and inclined to the ecliptic." Using a 50 power refracting telescope that he designed himself, Huygens also discovered the first of Saturn's moons, Titan.[18] In the same year he observed and sketched the Orion Nebula. His drawing, the first such known of the Orion nebula, was published in Systema Saturnium in 1659. Using his modern telescope he succeeded in subdividing the nebula into different stars. (The brighter interior of the Orion Nebula bears the name of the Huygens Region in his honour.) He also discovered several interstellar nebulae and some double stars.
Transit of Mercury
On 3 May 1661, he observed the planet Mercury transit over the Sun, using the telescope of telescope maker Richard Reeves in London together with astronomer Thomas Streete and Richard Reeves.[19]
Extraterrestrial Life
Christiaan Huygens believed in existence of extraterrestrial life. Prior to his death in 1695, he completed a book entitled Cosmotheoros in which he discussed his notions on extraterrestrial life. Huygens was of the opinion that life on other planets is similar to that on Earth. He thought that availability of water in liquid form was essential for life and therefore the properties of water should vary from planet to planet, since the kind of water that is found on Earth would instantly freeze on Jupiter and vaporize on Venus. He even reported observing dark and bright spots on the surface of planet Mars and Jupiter. This he explained could be justified only by the presence of water and ice on those planets.[20]
Works
- 1649 – De iis quae liquido supernatant (About the parts above the water, unpublished)
- 1651 – Cyclometriae
- 1651 – Theoremata de quadratura hyperboles, ellipsis et circuli (theorems concerning the quadrature of the hyperbola, ellipse and circle, Huygens' first publication)
- 1654 – De circuli magnitudine inventa
- 1656 – De Saturni Luna observatio nova (About the new observation of the moon of Saturn – discovery of Titan)
- 1656 – De motu corporum ex percussione, published only in 1703
- 1657 – De ratiociniis in ludo aleae = Van reeckening in spelen van geluck (translated by Frans van Schooten)
- 1659 – Systema saturnium (on the planet Saturn)
- 1673 – Horologium oscillatorium sive de motu pendularium (theory and design of the pendulum clock, dedicated to Louis XIV of France)
- 1673 – De vi centrifuga (Concerning the centrifugal force)
- 1684 – Astroscopia Compendiaria tubi optici molimine liberata (compound telescopes without a tube)
- 1685 – Memoriën aengaende het slijpen van glasen tot verrekijckers (How to grind telescope lenses)
- 1686 – Dutch: Kort onderwijs aengaende het gebruijck der horologiën tot het vinden der lenghten van Oost en West (How to use clocks to establish the longitude)
- 1690 – Traité de la lumière
- 1690 – Discours de la cause de la pesanteur (Discourse about gravity, from 1669?)
- 1691 – Lettre touchant le cycle harmonique (Rotterdam, concerning the 31-tone system)
- 1698 – Cosmotheoros (solar system, cosmology, life in the universe)
- 1703 – Opuscula posthuma including
- De motu corporum ex percussione (Concerning the motions of colliding bodies – contains the first correct laws for collision, dating from 1656).
- Descriptio automati planetarii (description and design of a planetarium)
- 1724 – Novus cyclus harmonicus (Leiden, after Huygens' death)
- 1728 – Christiani Hugenii Zuilichemii, dum viveret Zelhemii toparchae, opuscula posthuma ... (pub. 1728) Alternate title: Opera reliqua, concerning optics and physics
- 1888-1950 – Huygens, Christiaan. Oeuvres complètes. The Hague Complete work, editors D. Bierens de Haan (tome=deel 1-5), J. Bosscha (6-10), D.J. Korteweg (11-15), A.A. Nijland (15), J.A. Vollgraf (16-22).
- Tome I: Correspondance 1638-1656 (1888). Tome II: Correspondance 1657-1659 (1889). Tome III: Correspondance 1660-1661 (1890). Tome IV: Correspondance 1662-1663 (1891). Tome V: Correspondance 1664-1665 (1893). Tome VI: Correspondance 1666-1669 (1895). Tome VII: Correspondance 1670-1675 (1897). Tome VIII: Correspondance 1676-1684 (1899). Tome IX: Correspondance 1685-1690 (1901). Tome X: Correspondance 1691-1695 (1905).
- Tome XI: Travaux mathématiques 1645-1651 (1908). Tome XII: Travaux mathématiques pures 1652-1656 (1910).
- Tome XIII, Fasc. I: Dioptrique 1653, 1666 (1916). Tome XIII, Fasc. II: Dioptrique 1685-1692 (1916).
- Tome XIV: Calcul des probabilités. Travaux de mathématiques pures 1655-1666 (1920).
- Tome XV: Observations astronomiques. Système de Saturne. Travaux astronomiques 1658-1666 (1925).
- Tome XVI: Mécanique jusqu’à 1666. Percussion. Question de l’existence et de la perceptibilité du mouvement absolu. Force centrifuge (1929). Tome XVII: L’horloge à pendule de 1651 à 1666. Travaux divers de physique, de mécanique et de technique de 1650 à 1666. Traité des couronnes et des parhélies (1662 ou 1663) (1932). Tome XVIII: L'horloge à pendule ou à balancier de 1666 à 1695. Anecdota (1934). Tome XIX: Mécanique théorique et physique de 1666 à 1695. Huygens à l’Académie royale des sciences (1937).
- Tome XX: Musique et mathématique. Musique. Mathématiques de 1666 à 1695 (1940).
- Tome XXI: Cosmologie (1944).
- Tome XXII: Supplément à la correspondance. Varia. Biographie de Chr. Huygens. Catalogue de la vente des livres de Chr. Huygens (1950).
Portraits
During his lifetime
- 1639 – His father Constantijn Huygens in the midst of his five children by Adriaen Hanneman, painting with medaillons, Mauritshuis, The Hague
- 1671 – Portrait by Caspar Netscher, Museum Boerhaave, Leiden, loan from Haags Historisch Museum
- ~1675 – Possible depiction of Huygens on l'French: Établissement de l'Académie des Sciences et fondation de l'observatoire, 1666 by Henri Testelin. Colbert presents the members of the newly founded Académie des Sciences to king Louis XIV of France. Musée National du Château et des Trianons de Versailles, Versailles
- 1679 – Medaillon portrait in relief by the French sculptor Jean-Jacques Clérion
- 1686 – Portrait in pastel by Bernard Vaillant, Museum Hofwijck, Voorburg
- between 1684 and 1687 – Engraving by G. Edelinck after the painting by Caspar Netscher
- 1688 – Portrait by Pierre Bourguignon, Koninklijke Nederlandse Akademie van Wetenschappen, Amsterdam
Named after Huygens
Science
- The Huygens probe: The lander for the Saturnian moon Titan, part of the Cassini–Huygens Mission to Saturn
- Asteroid 2801 Huygens
- A crater on Mars
- Mons Huygens, a mountain on the Moon
- Huygens Software, a microscope image processing package.
- A two element eyepiece designed by him. An early step in the development of the achromatic lens, since it corrects some chromatic aberration.
- The Huygens–Fresnel principle, a simple model to understand disturbances in wave propagation.
- Huygens wavelets, the fundamental mathematical basis for scalar diffraction theory
- W.I.S.V. Christiaan Huygens: Dutch study guild for the studies Mathematics and Computer Science at the Delft University of Technology
- Huygens Laboratory: Home of the Physics department at Leiden University, Netherlands
- Huygens Supercomputer: National Supercomputer facility of the Netherlands, located at SARA in Amsterdam
- The Huygens-building in Noordwijk, Netherlands, first building on the Space Business park opposite Estec (ESA)
- The Huygens-building at the Radboud University, Nijmegen, The Netherlands. One of the major buildings of the science department at the university of Nijmegen.
Other
- Christiaan Huygens College, High School located in Eindhoven, Netherlands.
- The Christiaan Huygens, a ship of the Nederland Line.
- Huygens Scholarship Programme for international students and Dutch students
See also
References
- ^ Christiaan Huygens, Traité de la lumiere (Leiden, Netherlands: Pieter van der Aa, 1690), Chapter 1. (Note: In the preface to his Traité, Huygens states that in 1678 he first communicated his book to the French Royal Academy of Sciences.)
- ^ "GroteKerkDenHaag.nl" (in (Dutch)). GroteKerkDenHaag.nl. http://www.grotekerkdenhaag.nl/. Retrieved 13 June 2010.
- ^ "I believe that we do not know anything for certain, but everything probably." —Christiaan Huygens, Letter to Pierre Perrault, 'Sur la préface de M. Perrault de son traité del'Origine des fontaines' [1763], Oeuvres Complétes de Christiaan Huygens (1897), Vol. 7, 298. Quoted in Jacques Roger, The Life Sciences in Eighteenth-Century French Thought, ed. Keith R. Benson and trans. Robert Ellrich (1997), 163. Quotation selected by W.F. Bynum and Roy Porter (eds., 2005), Oxford Dictionary of Scientific Quotations ISBN 0-19-858409-1 p. 317 quotation 4.
- ^ p963-965, Jan Gullberg, Mathematics from the birth of numbers, W. W. Norton & Company; ISBN 978-0-393-04002-9
- ^ Christiaan Huygens, Traité de la lumiere... (Leiden, Netherlands: Pieter van der Aa, 1690), Chapter 1. From page 15: "J'ay donc monstré de quelle façon l'on peut concevoir que la lumiere s'etend successivement par des ondes spheriques,..." (I have thus shown in what manner one can imagine that light propagates successively by spherical waves,...)(Note: Huygens published his Traité in 1690; however, in the preface to his book, Huygens states that in 1678 he first communicated his book to the French Royal Academy of Sciences.)
- ^ "Boerhaave Museum Top Collection: Hague clock (Pendulum clock) (Room 3/Showcase V20)". Museumboerhaave.nl. http://www.museumboerhaave.nl/AAcollection/english/M03V20_V09853.html. Retrieved 13 June 2010.
- ^ "Boerhaave Museum Top Collection: Horologium oscillatorium, siue, de motu pendulorum ad horologia aptato demonstrationes geometricae (Room 3/Showcase V20)". Museumboerhaave.nl. http://www.museumboerhaave.nl/AAcollection/english/M03V20_g13604.html. Retrieved 13 June 2010.
- ^ Marin Mersenne 1647 Reflectiones Physico-Mathematicae, Paris, Chapter 19, cited in Mahoney, Michael S. (1980). "Christian Huygens: The Measurement of Time and of Longitude at Sea". Studies on Christiaan Huygens. Swets. pp. 234–270. http://web.archive.org/web/20071204152637/http://www.princeton.edu/~mike/articles/huygens/timelong/timelong.html#_N_13. Retrieved 07 October 2010.
- ^ Matthews, Michael R. (2000). Time for science education: how teaching the history and philosophy of pendulum motion can contribute to science literacy. New York: Springer. pp. 124–126. ISBN 0306458802. http://books.google.com/?id=vCtYnEuW7TIC&pg=PA126&dq=mersenne+isochronism+pendulum#v=onepage&q=mersenne%20isochronism%20pendulum&f=false.
- ^ T. Birch, "The History of the Royal Society of London, for Improving of Natural Knowledge, in which the most considerable of those papers...as a supplement to the Philosophical Transactions," vol 2, (1756) p 19.
- ^ A copy of the letter appears in C. Huygens, in Ouevres Completes de Christian Huygens, edited by M. Nijhoff (Societe Hollandaise des Sciences, The Hague, The Netherlands, 1893), Vol. 5, p. 246 (in French).
- ^ Hans van den Ende: "Huygens's Legacy, The Golden Age of the Pendulum Clock", Fromanteel Ldt., 2004,
- ^ van Kersen, Frits & van den Ende, Hans: Oppwindende Klokken – De Gouden Eeuw van het Slingeruurwerk 12 September – 29 November 2004 [Exhibition Catalog Paleis Het Loo]; Apeldoorn: Paleis Het Loo,2004,
- ^ Hooijmaijers, Hans; Telling time – Devices for time measurement in museum Boerhaave – A Descriptive Catalogue; Leiden: Museum Boerhaave, 2005
- ^ No Author given; Chistiaan Huygens 1629-1695, Chapter 1: Slingeruurwerken; Leiden: Museum Boerhaave, 1988
- ^ nature – International Weekly Journal of Science, number 439, pages 638-639, 9 February 2006
- ^ Notes and Records of the Royal Society (2006) 60, pages 235-239, 'Report – The Return of the Hooke Folio' by Robyn Adams and Lisa Jardine
- ^ Ron Baalke, Historical Background of Saturn's Rings
- ^ Peter Louwman, Christiaan Huygens and his telescopes, Proceedings of the International Conference, 13 – 17 April 2004, ESTEC, Noordwijk, Netherlands, ESA, sp 1278, Paris 2004
- ^ "Johar Huzefa (2009) Nothing But The Facts – Christiaan Huygens". Brighthub.com. 28 September 2009. http://www.brighthub.com/science/space/articles/50441.aspx. Retrieved 13 June 2010.
Further reading
- Andriesse, C.D., 2005, Huygens The Man Behind the Principle. Foreword by Sally Miedema. Cambridge University Press.
- Boyer, C.B.: A history of mathematics, New York, 1968
- Dijksterhuis, E. J.: The Mechanization of the World Picture: Pythagoras to Newton
- Hooijmaijers, H.: Telling time – Devices for time measurement in Museum Boerhaave – A Descriptive Catalogue, Leiden, Museum Boerhaave, 2005
- Struik, D.J.: A history of mathematics
- Van den Ende, H. et al.: Huygens's Legacy, The golden age of the pendulum clock, Fromanteel Ltd, Castle Town, Isle of Man, 2004
- Yoder, J G., 2005, "Book on the pendulum clock" in Ivor Grattan-Guinness, ed., Landmark Writings in Western Mathematics. Elsevier: 33-45.
- Christiaan Huygens (1629-1695) : Library of Congress Citations. Retrieved 2005-03-30.
External links
Primary sources, translations
- Works by Christiaan Huygens at Project Gutenberg
- Treatise on Light translated into English by Silvanus P. Thompson, Project Gutenberg etext.
- De Ratiociniis in Ludo Aleae or The Value of all Chances in Games of Fortune, 1657 Christiaan Huygens' book on probability theory. An English translation published in 1714. Text pdf file.
- Horologium oscillatorium (German translation, pub. 1913) on the pendulum clock
- ΚΟΣΜΟΘΕΩΡΟΣ (Cosmotheoros). (English translation of Latin, pub. 1698; subtitled The celestial worlds discover'd: or, Conjectures concerning the inhabitants, plants and productions of the worlds in the planets.)
- Traité de la lumière or Treatise on light (English translation, pub. 1912 and again in 1962)
- Systema Saturnium 1659 text a digital edition of Smithsonian Libraries
- On Centrifugal Force (1703)
- Huygens' work at WorldCat
- Christiaan Huygens biography and achievements
- Portraits of Christiaan Huygens
Museums
- Huygensmuseum Hofwijck in Voorburg, Netherlands, where Huygens lived and worked.
- Huygens Clocks exhibition from the Science Museum, London
- LeidenUniv.nl, Exhibition on Huygens in University Library Leiden (Dutch)
Other
- O'Connor, John J.; Robertson, Edmund F., "Christiaan Huygens", MacTutor History of Mathematics archive, University of St Andrews, http://www-history.mcs.st-andrews.ac.uk/Biographies/Huygens.html.
- Huygens and music theory Huygens–Fokker Foundation —on Huygens' 31 equal temperament and how it has been used
- Christiaan Huygens on the 25 Dutch Guilder banknote of the 1950s.
- Christiaan Huygens at the Mathematics Genealogy Project.
- [1] How to pronounce "Huygens"